Category: Poser

One major issue that came up when discussing Cloth Room in the Renderosity forum was crumbling, very well documented by Bagginsbill.

 

Let’s consider a quad mesh, with the edges in horizontal and vertical (or: UV-) direction. Stretching, folding and shearing in those directions happen in a straightforward way. So let’s look when forces are applied diagonally.

When pushing, the cloth might fold diagonally without having direct counterforces available: no edges, hence no springs. Shear and fold work against it a little bit, but generally are not strong enough to push all the surrounding cloth away. So it’s easy to bring the opposite vertices together. This is exactly what causes the “crystal ridges” as artifacts in the cloth. And for quads those ridges can exist in both diagonal directions, so crumbling is caused when some of those ridges come together and combine effects.

This is different in tris, which have a diagonal edge in at least one direction. So mono-tris still might ridge in one direction but are hard to crumble, X-tris, Zigzags and Hexes can resist ridge forming in all directions and won’t crumble.

What might help against ridges in quad meshes?

• Not using quads resolves this to some extent, and smaller quads make smaller ridges
• Increasing shear and/or fold resistance will push the crumbles out. But high shear and fold resistance will affect other behavior of the cloth as well, life is a compromise. Reducing mass (density), friction and other effects will make this pushing more successful. So instead of raising fold/shear resistance, reducing density is an option. And as shear and fold resistance work together in this case, you can do with less fold and more shear.

Engineering stuff

For those who like the formulas for a better understanding.

Consider a quad, three vertices in a plane, the fourth one out of plane. If the distance to its opposite vertex (in the same poly) is 100% in case the vertex IS in plane, then now it’s shorter: X% instead. When X=0 the quad has folded completely into a double sided triangle.

In this out-of-plane position, this quad and its neighbors make a shearing force S*(90-a) with S the shearing resistance (equal or related to the Poser parameter, one never knows) and a the angle between two adjacent edges (orange, in the scheme). At a=90° (perpendicular), shearing is null while each deviation generates deformation of the quad and counterforces accordingly.
The quad and neighbors also make a folding force F*(180-b), with folding resistance F and b the angle between opposite edges (pink in the scheme). At 180° the edges are in line, no folding, and any deviation generates folds and counterforces accordingly.

From geometry, we’ll have Sin(a/2) = ½ * sqrt(2) * X and Sin(b/2) = ½ * sqrt(2) * sqrt( 1+X² )

For each X there is a valid combination a and b (see the graph), so for each X there is a ridge-resisting force. The ridge only disappears when this force is larger than the counterforces for friction and gravity.

At the left, say X=90%, we find (180-b)=40 and (90-a)=10, a 4:1 ratio between (anti)folding and (anti)shear. Halfway, at 50% we’ll find a 1.5:1 ratio. So when reducing the (anti)folding with 1, the (anti)shearing force should go up with at least 4 to 1.5 to get a similar result. Otherwise things get worse.

Via the sim mechanisms and via the cloth parameters, the real world is sneaking into our comfortable and manageable virtual Poser environment. This implies that understanding the real world enhances our abilities to handle Cloth Room, and vice versa, handling Cloth Room requires the understanding of the real world. Which brings the high school books on geometry and mechanics on our desk.

I like that, I got my MSc in that arena (a very long time ago). You might not, no apologies needed. Just pick up the clues, the results, and skip the intermediate steps. I’ll mark them as clear as possible. You might like it, to some extent, but you may consider to skip the advanced parts. No apologies needed for that too. I’ll mark the advanced steps as clear as possible as well. When there are a lot of them, I’ll put them in separate chapters but sometimes I don’t. Simply because it’s a bit annoying to scatter a single subject all over the tutorial.

A word of warning on all the details. In the previous chapter Cloth parameters – the Sim Side I’ve discussed that

• It’s not the values themselves but the ratios between them that make the difference, especially when considering Density, the Dampings and the Resistances.
• When the values hamper a decent progress of the calculations or hamper the creating of a good result, then change them (while keeping the ratios if possible). Some cloth may look like leather and drape like leather and behave like leather, but that’s only relevant when the sim comes to an end in due time and shows a decent result by itself.
• So, the real world values are mainly of help to obtain reasonable parameter sets for cloth materials. Nothing less, nothing more.

And on top of that, the cloth sim itself resembles some workings from nature, following the laws of physics. Understanding of that can help to understand the sim, and hence might be valuable to make the changes where we need them to get the desired results. And to make them more efficiently and effectively, without endless trials and errors.

In the meantime, in might be profitable to understand more about cloth in general. Just cotton will do, I guess. Two Wikipedia articles might open, or close, your eyes:

• http://en.wikipedia.org/wiki/Textile_manufacturing on the process from cotton to textile
• http://en.wikipedia.org/wiki/Units_of_textile_measurement on Denier, tex, diameters and more

while another article might give a nice overview or insight in textile properties:

• http://na1.northsails.com/North_Cloth/fiber_properties.html as seen by a high-performance sail maker

Most Poser Rooms are on the details of scene building, and Pose Room itself is all about virtuality. Size does hardly matter, when everything is doubled in size you still might get the same result. Things are relative (with a few exceptions, like some parameters in the new scatter node and some camera settings).

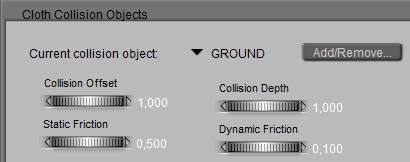
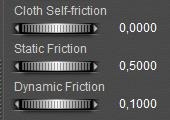
Cloth Room is different. Although the Stretch, Fold and Shear parameters define the behavior of cloth related to itself, and the Friction parameters define the relationship between cloth and the objects in the scene, the Cloth Density and Air Damping introduce real concepts like gravity and an surrounding atmosphere filled with air. They cannot be turned off, and are the essential driving forcing of everything that further happens in the Cloth Room. No sim without gravity. So let’s start there.

Density and gravity

In Cloth Room, take a piece of cloth, pump up the density (increase mass) as well as the Fold etc. resistances (stiffen it), zero the Air Damping to eliminate the air-effects, drop it from some height and look up your high school mechanics formulas, and the Earth gravitational constant. They apply. Use 30 animation frames for 1 second, and you can predict when the thing hits the floor.

H = 1/2 * g * f² or f = sqrt(2*H/g) with height H in cm, gravity constant g equals 1,089 cm/f² and f the time in frames.

In detail: Earth gravity reads 9.800 m/s² on the Earth surface. There are differences, it’s 9.832 at the poles and 9.780 at the equator as the Earth is not a perfect ball, and it varies a bit with underground and surroundings too. But 9.800 is a decent average. That value, converted to 100cm/m, equals 980 cm/s² and another conversion to 30fps makes 1.089 cm/f².

Density in Poser is grams per cm², 1 g/cm² equals 10kg/m² which equals 10.000 kg (10 tons) per m³ for a sheet 1mm thick. Office paper is “80 grams”, per m² that is. A0 flip over / poster size is 1 m². I’m a 6 feet guy , I guess my summer pants take about 1 m² = 10.000 cm² of cloth, when I put them on a kitchen scale it reads say 250 grams. So the Poser setting would be 0.250. Just measure up your own clothes, and you know. These are my findings:

Thin shirt, Wooden tie.

Air Damping and Wind

Air resistance is similar. Ignoring units for the moment it’s the force generated by an air flow of 1 m/s through (or at) a 1 m² cloth surface. I can measure it. I take a cylinder (Poser primitive), make it long enough, put it horizontal as a flag pole, and attach a piece of cloth. I just collide it to the pole, and put one row of vertices in the constraints group. Now I’ve got a flag. Or I lose the pole and put the upper row of vertices in the choreographed group. Same to me.

I drape it, after some frames it will hang down properly. Now I can apply wind force, from the menu, let’s make it from aside. The wind will blow it aside, gravity will pull it down and the angle that results from the simulation tells me the relationship. I vary air resistance and density and the angle will exactly vary as expected. We’ll do that later.

First I redo the dropping experiment. I take the cloth up but now I give it meaningful density and air resistance values. Like the default ones, which are suggested for table cloth. I drop it (now the cloth moves, instead of the air, doesn’t matter), and note that it takes a bit longer to hit the floor. If I drop it from larger heights, and note the intermediate results, I can observe that it reaches a constant velocity going down. The cloth moves through the air, the resistance generates a force upward. Gravity pulls it down, and increases the velocity. Therefore, the air resistance force will increase, until it equals gravity. Then the forces are in equilibrium, and the thing will not accelerate any more.

Just another way of deriving the air resistance value, as the final steady speed v (cm/s) reads: v = g *d / a

For speed in cm/s, gravity g (980 cm/s²), density d (gram/cm²) this implies air damping a to be in gr/cm² per second.
And for the Poser default values d = 0.005 and a = 0.02, I get v = 980 * 0.005/0.020 = 245 cm/s

So now I understand air resistance, in its simplest form, and I can check out the Wind Generator using the flag as described above. I give the cloth maximum stiffness (fold etc), zero friction, and default density and air resistance.

Then I put a Wind Force generator aside, and make it blow straight into the cloth. I give it some distance (twice the cloth size will do), leave the generator angle at 45°, and give it a serious range (4 to 5 times the cloth size will do). A Wind generator is quite a rude thing actually. It will produce the full force in an area determined by angle and range, and nothing outside it. No fall offs like spotlights. I leave the Amplitude at 1, the question is what that means.

So I run the sim, and find the flag hanging at an angle of 45°.

Now I know what’s meant by Amplitude = 1. That’s the wind that – when blowing horizontally – will push a default piece of cloth up with the same force that is exercised by gravity to pull it down.

More precise, a wind speed w will hang the flags at angle z, where w = g * d/a * sin(z)/( 1-sin²(z) ).
So when the flag hangs 45* for the default values d= 0.005 and a=0.02, then Windforce amplitude 1 implies w = 348 cm/s.

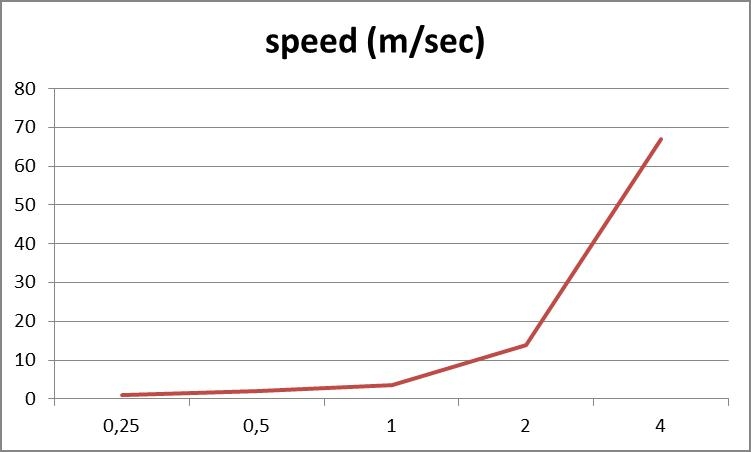
What will happen to the wind speed when I adjust Amplitude? For this, I had to repeat the sim at various amplitude settings.

• Amplitude 2 created an angle of 66,5, that’s a windspeed of 1360 to 1400 cm/s, that’s about 4 times as fast.
• Amplitude 4 created an angle of 80-78, that’s a windspeed of 8000 – 5500, or: another 4 times as fast again.
• Amplitude 0.5 gave an angle of 34, that’s 199.3 (say 200) cm/s, or roughly half as much compared to amplitude 1.
• And Amplitude 0.25 gave an angle of 22, windspeed 106.7 (say 100) cm/s, or another half as much again.

It looks like the amplitude and windspeed relate in a linear way below amplitude 1 or a 45* flag angle (half the amplitude gives half the windspeed), and relate in a squaring way (double the amplitude quadruples the windspeed) above amplitude 1 or a 45 flag angle. This gives artists more control in both regions, as if the dial changes sensitivity.

Wrap up

Gravity acceleration in Poser is 980 cm/s². It is slightly different from the one used in the Gravity script from the Scripts menu, so take care when mixing results from both. I’ve not looked at the Poser Physics application yet.

Density in Poser is gram/cm², so the default 0,0050 means 50 grams/m², about half the value for office paper and good for light silk. The max 1.0 means 10 kg/m² which is about a sheet of lead of 1 mm thick, or a piece of usual cloth material, 1 cm think.

Air damping in Poser is gram/cm² per second. An object that feels a force will accelerate, the air damping will increase with velocity, and this results in a maximum speed for the cloth relative to the wind/atmosphere. So when my figure is wearing a gown, and some body parts are moving at about or above this speed limit, we can expect the cloth sim to break or to show that the other forces have to work hard to make it possible.

For a force of 1G (normal gravity pull) this speed is v = g*d/a for the Poser dial values d (density) and a (air damping). So our default light silk reads: v = 0,005 * 980 / 0,02 = 245 cm/s (=> 2,45*100/30) = 8,16 cm/frame. So, at this speed the cloth feels a windforce with is equal to the gravity force pulling it down.
245 cm/s is pretty fast, but sometimes our animation moves about the same speed or faster and then the cloth is facing windforces of 1G or more. For instance, if my 180cm large figure in the scene makes a cartwheel then the feet will travel a distance of 2*pi*180/2 = 565cm in say 0.7 sec gives 800cm/s and hence a long skirt requires a 3.3G force at ankles height to move forward. Such a force requires high values for Stretch and Shear resistance and a large number of steps per frame in the calculations to prevent is from ripped apart in the sim. The good news is that the cloth will be pushed against the legs with that same force, so we’ll need only a little bit of friction to keep it in place.

Windforce amplitude in Poser represents windspeed in cm/s, that is : amplitude 1 applied horizontally to a cloth of default material (light silk) pulled down vertically by gravity, will bring the cloth into a 45 degrees angle. That results in : 346 cm/s. For amplitudes below 1 the dial behaves in a linear way, so 0.5 implies half the windspeed. For amplitudes above 1, doubling the dial value quadruples the windspeed. This translates into :

• amplitude 0,10 is the upper limit of Beaufort 0, calm, smoke plumes going up straight
• amplitude 0,50 is the upper limit of Beaufort 1, light air, smoke plumes tell the wind direction
• amplitude 1,00 is the upper limit of Beaufort 2, light breeze, feel the wind, leaves whisper, minor seawaves
• amplitude 1,25 is the upper limit of Beaufort 3, waving flags, whirling dust, moving leaves
• amplitude 1,50 is the upper limit of Beaufort 4, waving hair, whirling paper and fierce moving leaves
• amplitude 1,75 is the upper limit of Beaufort 5, moving branches
• amplitude 2,00 is the upper limit of Beaufort 6, strong breeze, problems with your umbrella, large seawaves
• amplitude 2,25 is the upper limit of Beaufort 7, hard wind, really hard to walk of cycle against the wind
• amplitude 2,45 is the upper limit of Beaufort 8, stormy, falling twiggs
• amplitude 2,65 is the upper limit of Beaufort 9, storm, falling branches and (roof)tiles
• amplitude 3,00 is the lower limit of Beaufort 12, hurricane

All this is relevant for those who want to combine poses, moves, cloth sims and falling props into one believable shot. The max value 4 seems nice for extreme comic scenes, the wind will turn you inside out.

For instance: at amplitude 2, the wind speed is 3,46 * 2² = 13,84 m/s. At default cloth density and air damping, this will exercise a force of 13,84 / 2,45 = 5,65 G’s on the cloth (see above, a force of 1G relates to a windspeed of 2,45m/s). Gravity G times 5,65 requires a figure working very hard to walk slowly forward against the wind, and also requires large stretch resistance values to prevent the gown from being shred in pieces.

So I do hope that some understanding not only enables you to make believable dynamic clothes, but also to make believable dynamic pictures.

Reality check

Let’s reconsider some Poser default values.

The default cloth density reads 0.005 which represents light silk. From the measurements however it appears that the tenfold, 0.050, is a better representation for normal cloth. A quarter of that (0.012) for lace, half of that (0.025) for thin clothing (thin shirt, summer dress), one-and-a-half of that (0.075) for thick cloth (jeans).

Now, I hang my flag down. In my observation, a Beaufort 3 is required to skew my flag (density 0.02, see table) at at most 30*, that’s about 540 cm/s wind speed while sin(z)=0.5.

Using the mentioned formula w = g * d/a * sin(z)/( 1-sin²(z) ) I get a = 980 * 0,02 / 540 * 0,5 / (1-0,25) = 0,024 instead of the default 0,02. So regarding to the flag the default Poser cloth density is fourfold too low, and the default Poser air damping is just a bit too low as well.

Note, as you can see in all formulas, it’s the ratio d/a that comes back each time. This means that when I change them in sync I’ll get the same physical results. For the default setting, this ratio is 0.005/0.02 = 0.25. For my flag it’s 0.02/0.024 = 0.83. I can also rephrase this as: regarding to the flag, the Poser default stuff offers far more air damping for is density. Which is quite an adequate description of the tight woven light silk, which gently floats down when I drop it above the floor.
Hence, I either set my density to 0.02 and the air damping to 0.024 or I leave the density at its default 0.005 and reduce the air damping to 0.006. For flags that is. Change things when you do know different. Just for making waves on a little bit of wind, flags have a higher air damping than standard linen. Light silk also is different, silk is known for its specific high air damping due to its very tight weave: it hardly lets the air pass through.

So as far as I can see now, Poser default represents light silk. Not table cloth, not flags, not heavy cloth covering cars and statues, not shirts, not jackets, not jeans, not medieval gowns. Light silk.

As far as you consider the use of wind force for some extra dynamics in the scene (like photographers are using a wind machine as well during photo shoots): meaningful amplitudes are between 0.5 and 1.5, and the default 1.0 is a very reasonable default.

Living in another world

Poser Cloth Room is supposed to represent Earth surface, as I can find a decent fit for its gravity and atmospheric density, from cloth drop and flag tests (see next section). This makes me curious: can I mimic other environments as well? It would be handy to have dials for gravity and atmosphere, but there aren’t.

On the Moon, gravity is low (16.7% of Earth), and so it’s on Mars (37.7%). On Jupiter, it’s large (236%). Venus and Saturn have about Earth values. Under water, there is an additional upward force (lowering gravity for the moment) which is proportional to the difference in density between the object and its surrounding water. But since cloth is organic, there is not that much of a difference, except for clothes that are filled with air initially. Fleeces, woolen knits and thick weaves for instance. When the air is gradually replaced by water, they sink like the rest. So for well dressed mermaids, I don’t have to correct for gravity.

To mimic low gravity, I can either increase all parameters except density (for the moon: 1/16.7% = 6-fold), or do the reverse. That is: reduce density (for the moon: 16.7% of the initial value), increase the frictions anyway (!) and leave the other parameters alone. To mimic high gravity, I can either reduce all parameters except density (for Jupiter: to 1/236% = 42%), or do the reverse: increase density (to 236% of the initial value), reduce the frictions anyway and leave the other parameters.

On the Moon and on Mars, the low gravity results in a low atmospheric density as well. Jupiter is different, it’s a gas planet without a surface, it just gets denser the way in. Its “ground level” is defined as the level where the atmospheric pressure equals 1 (Earth) atmosphere, and its composition is very light (mainly hydrogen and helium). But we might want to do high densities anyway. Like under water, where moving cloth definitely is something different. The basic idea is: I just have to reduce (thin atmosphere) or increase (thick atmosphere) the Air Damping, and I’m done.

The Moon effectively has no atmosphere at all, so air damping can be zeroed out. The Mars atmosphere has a low pressure (0.01 Earth atmosphere), but is quite thick thanks to the carbon dioxide and so it supports serious winds and dust storms. I tend to reduce Air Damping to 10%, like I would for Jupiter for its thin atmosphere. Venus on the other hand is extremely hostile, with an thick carbon dioxide and sulfuric acid atmosphere, temperatures from 400 to 700K and an atmospheric pressure of about 90 Earth atmospheres. Not for tourists. Air damping needs to be tenfolded or – like under water – hundredfolded for realistic results, which will bring me at the limits that the sim will support. But I can also reduce the density, and the other parameters (except the frictions) instead. Because it’s the ratio that counts in the sim result.

The issue with large (relative to density) Air Damping, is that it limits the speed which one can move. We know all that, from our attempt to run in a shallow pool, or from attempts to swim with our daily clothes on. The Cloth Room is not different. In real life, the cloth will hamper our movements and we’ll need serious forces to get the job done. If the cloth cannot stand the forces, the fibers will snap and the cloth will tear. In Poser, figures can apply unlimited forces onto the cloth, and its fibers won’t snap. But I’ll need a hell of a Stretch Resistance to keep the cloth in decent shape under those forces, and so things tend to grow out of hand. Many Steps per Frame, and so on. A better way is to slow down the movements, or even reconsider them. Again, if it’s hard to do in real life, then it’s hard to get it done properly in Cloth Room as well.

Engineering stuff

In this section I’ll present some further details on gravity, and handling air damping. For those who did well in physics class, and want to verify (and approve upon) my findings.

On gravity, I’ve noted that the Gravity Script (in Menu > Scripts > Utility) not only let the object bounce (with 50%) on the floor, and on the floor only (Y=0) without any possibility to alter things, but also contains the code lines:

• g = – 0.005        \ this is the Earth gravity acceleration in the script
• loop :
  • v = v + g    \ velocity starts at 0, and increases downwards on a per frame basis
  • y = y + v        \ height starts at Y in scene, and decreases on a per frame basis

in that order.

Some things are wrong here:

• in the script, gravity is expressed in Poser Native Units (1PNU=262cm) per frame squared. From the metrics g=9,80m/s² this means 0.00416 for 30fps or 0.00598 for 25fps. The value used in the scripts is about the average of those, so the result is about equally inaccurate in both popular playback speeds. It also deviates from the Cloth Room value which exactly matches the Earth value of 9,8 m/s² on 30fps.
• The second phrase is correct, it determined the velocity at the end of each frame. But the third phrase misses the point that it should use the average velocity during the frame period, and not the end value. So actually it should read: y = y + (v-g/2). As a result the object displaces too much per frame, it moves too fast according to its speed, and according to the laws of physics. This comes on top of the error in the gravity value itself. For 25fps these errors might cancel out a bit, but for 30fps the errors add up.

So it’s a fun, but inaccurate script which might reveal its surprises the moment you use it next to your cloth sims in the same scene.

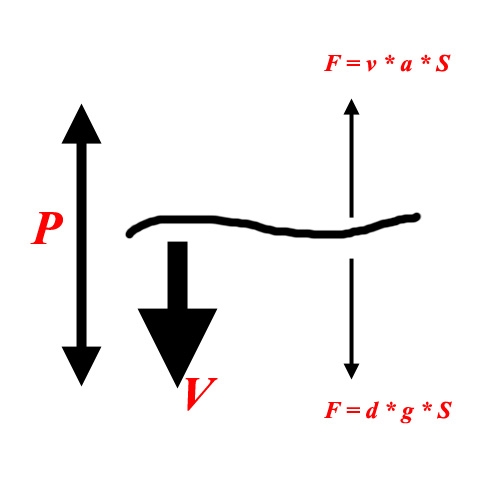
On air damping, air is flowing through a piece of cloth, at some velocity v. There is an air pressure difference P between both sides of the cloth. The ratio between those is the air resistance, a. Then P = v * a.
For those into electronics: it’s similar to Ohm’s law, Voltage V, current I, resistance R: V = i * R. Only this time, air is flowing instead of current.

The air pressure (difference) creates a force perpendicular to the cloth, proportional to the amount of cloth (surface S):

F = P * S (add in P=v*a) = v*a*S

Now, consider our drop-drown experiment. There is no atmospheric movement but the cloth is flat falling down at speed v, same effect, same force. But initially, the cloth is dragged down by gravity, at a force F=d*S*g . Same surface S, mass density d (kg/m2) and Earth gravity acceleration g.
While the gravity pulls the cloth down, it accelerates, speed increases, upward air damping force increases and finally, both forces equal out. From then on, the cloth falls down unaccelerated, at constant speed.

From the equations we can see that from that moment a*S*v = d*S*g. The surface cancels out as the result is the same for any size of cloth (and any shape, as long as it falls flat). And the final speed reads v = g * d / a.

When v is in m/s and g in m/s², then the ratio d/a is in sec. All other units in d and a should be similar, so if d is in g/cm2 as the Poser manual tells us, then a is in g/cm² too – per second. For v in cm/frame and a per frame as well, gravity should be in cm/f² (value 1,089).

We know the basic formulas for non-damped motion:

• acceleration g, which is a constant
• speed v = g * t, increasing at constant rate over time t
• displacement h = 1/2 * g * t²

Now for air-damped motion:

• acceleration g – v * a/d, gravity minus air damping, it varies with speed v itself. So
• speed v = d*g/a * [ 1 – e ^{( -a/d * t)} ] and therefore
• displacement h = d*g/a * { t – d/a * [ 1- e ^{( -a/d*t)} ] }

Now back to Poser. I took my cloth, raised it to 19,6 mtr, set folding etc to the max to make it stiff as a marble plate, but kept density and air resistance at default values. That’s 0.005 gram /cm² for density and 0.02 gram/cm² per second for air resistance. The ratio a/d reads 0.020/0.005 = 4 /sec, and that implies that at 1 sec, the exp(…) part in the formula is reduced to less than 2% and can be ignored, to simplify calculations.
That means: 19,6 mtr = 0,25 * 9,8 * ( t – 0,25) or : impact at 8,25 sec, that’s just beyond frame 247 (poser time in cloth room is always 30fps, whatever your animation settings). That’s theory.

Sim run. Drop down. At frame 247 it’s just above the ground, at frame 248 it has had the full hit. That’s Poser reality meets theory. Great.

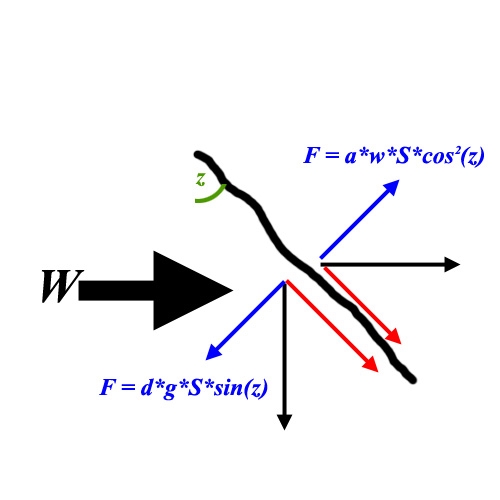
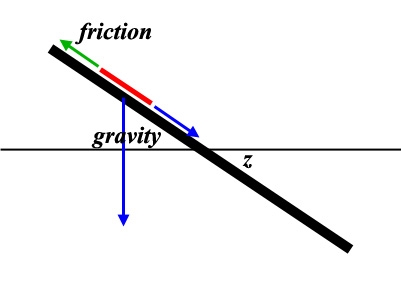
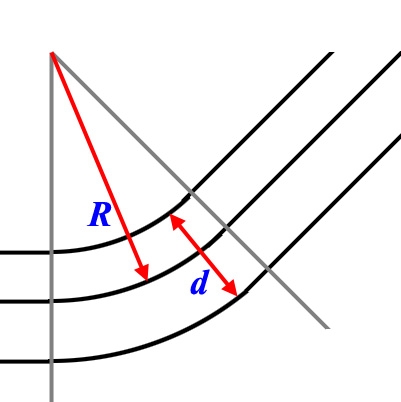
On Wind force, let’s do the math first too. Take angle z as the angle between the flag and the vertical. Z = 0° means hanging down, no winds, and z=90° means a horizontal flag, extreme winds.

The (vertical) gravity force on the skewed flag can be decomposed in a part along with the flag, stretching it and being countered by the pole (if we had one), and a part perpendicular to the cloth, making it rotate downwards. This latter force is F = d*S*g*sin(z), d for mass density, S for cloth surface, g for gravity acceleration constant.

The (horizontal) wind force has a similar effect, but we have to adjust for the fact that a skewed flag will present a smaller surface to the wind. Again, the force can be decomposed into one along the flag stretching it as well (you know cloth is pulling when the wind blows in), and a force perpendicular, rotating it upwards:

F = a*S*w*cos² (z) with airdamping a, windspeed w (in m/s), surface S and the cosine squared thanks to the mentioned adjustment.

The flag hangs at equilibrium when both rotational forces cancel out, and since cos² equals 1-sin², we can make it to

0 = a*w*sin² (z) + d*g*sin(z) – a*w

From this we learn that when airdamping a or windspeed w equal zero (no atmosphere, or no wind) then the equation reduces to sin(z) = 0, z = 0°, flag hangs down. And we learn that when a and/or w grows really big (under water, hurricane) then the equation reduces to sin(z) = 1, z=90°, flag fully stretched horizontally.

From this we can determine the meaning of Amplitude 1: we just solve the equation for z=45° and find a windspeed of 3,46 m/s. Default density at 0.005, default airdamping at 0.02.
Now I know windspeed, air-damping, mass density and the gravity constant values, I can easily predict the angle or calculate windspeed by solving the generic equation above:

sin(z) = { -d*g + sqrt[ (d*g)² + (2*a*w)² ] } / (2*a*w)
or w = d*g/a * sin(z) / [1- sin² (z)]

Note that the cases a*w= about 0 or a*w= really large already were discussed above.

I ran my sims for 100 frames at various Windforce Amplitudes, flags were still waving a bit at the edges (they make a full wave despite the extreme stiffness settings) but still enough to make estimates of the angles. From these angles I got the windspeeds, and now I know the relationship between Amplitude and Windspeed.

When a piece of cloth lies down on the floor or on something else, and a force – like gravity – is applied on it to drive it forward, then the contact of that cloth with the floor will work against it. Up till some limit the cloth won’t move at all, that limit is called the static friction. When that limit is exceeded it will move but will still apply a force against it. This latter is called dynamic or kinetic friction. Generally, dynamic friction is less than static. Friction is a surface quality only, it does not depend on cloth density nor on the cloth speed over the surface. It is said that rough surfaces have more friction, but that might be as well the other way around: cloth with more friction is experienced rougher. It is said that alike surfaces have more friction than surfaces which are far from similar, which is why insects can walk on vertical glass panels. It is said that surface structure from a geometrical point of view has not that much impact, friction is the result of (electrostatic) forces between the surface molecules. Take your pick. For Poser use, let’s stick to the roughness concept for the sake of it.

Total friction in green, Static portion in red, dynamic portion in blue.

An experiment the get a feel for friction is easy to do at home. Clean up a smooth long table, or a smooth plank, put a piece of cloth flat on one end and tilt the table. Until some tilt angle is reached, the cloth will stay put. That’s static friction. When the tilt becomes larger than that, the cloth starts to move smoothly. That’s dynamic friction working against the gravity pulling it down.

Poser Friction

In Poser, friction comes in various flavors:

• Static and Dynamic between cloth element and collision object, from the collision object point of view.
  It sort of states the roughness of the surface of the collision object. These parameter values can be set in panel 2, where I manage the collision objects. Each object from the list has its own settings.
• 
  Static and Dynamic, from the cloth element point of view, it’s about the roughness of the cloth surface. These values can be set in panel 4, where I manage the cloth behavioral details.
• Self-friction between cloth elements themselves, which is always about cloth surfaces.

For the moment I’ll concentrate on Static and Dynamic and leave Self-friction alone. Just leave it at 0 in the parameters panel, no harm done.

In life, friction not only depends on surface structures but also on complex interactions. Silk might do smooth and fine over glass and female bodies, but can turn in disaster when moving over plastics due to electrostatics, or when moving over brushed aluminum because the fine surface structures seem to ‘fit’.
In Poser I can define frictions for the object as well as for the cloth, but I’ve got to tell Poser which ones to use in the calculations.

If I tick the Collision Friction box in panel 4, then this particular cloth element will experience the friction as defined for each collision objects it will be sliding over.
If I uncheck the box, then all collision elements will experience the friction as defined for this piece of cloth.

So, the friction values for a specific collision object hold for the interactions with all cloth elements that will slide over it – as long as these cloth elements have their Collision Friction ticked. And the friction values for a specific cloth element hold for the interactions with all collision objects that it will slide over, when its Collision friction is not ticked. Hence, there is no combination of values that takes object roughness, cloth roughness as well as some interaction into account.

For example:
the girl in my scene wears a silk blouse and a long leatherish skirt. The skirt collides to the ground as well, which is covered with a rough carpet. For the skirt, the friction with the girl and with the ground drastically differ and I want to show that, so for the skirt I tick the Collision Friction box and I assign the girl and the carpet appropriate values, the latter substantially larger than the former. For the blouse I can’t check the box too, as the friction of silk with the body differs too much from the friction of the skirts leather with the body. So I leave the box unticked and I give the blouse its own – rather low – silky friction values.

Friction is important for cloth room. While density (gravity) and air-resistance address the interaction between the cloth and the room itself, friction addresses the interaction between the cloth and the figure it collides with. Simply stated: when the cloth vertices hit the figure in a perpendicular way we’re talking collision, and when they interact in a parallel way, we’re talking friction. So friction might be as relevant as collision. Might not be so much for still images, but it certainly plays a relevant role in believable animations using dynamic clothes.

Finding real world values

With a flattened and stretched box and a square piece of cloth, I just rebuild the “tilted plank” experiment mentioned above. And after each run of the sim, I gathered positions for the various frames in the animations. Position changes over time make velocity, velocity changes over time make acceleration.

For this acceleration a, I know that a = G*sin(z) – D*cos(z) for tilt-angle z (with the horizon, as set in Z-Rotate), for dynamic friction effect D (under investigation) and for gravity acceleration G = 9.8 m/s² = 1.089 cm/f² when switching to the Poser Cloth Room units cm and frames, at 30 fps. That’s basic mechanics.

The question is: how does D in this theory relate to the setting in the Poser cloth parameters?

Well, it IS the setting !! The Poser dynamic friction is not a dimensionless ratio between forces as in the physics literature, it is the resisting acceleration from the cloth on to some surface (or the other way around, in the collision object properties), under Earthy gravity, expressed in Poser Cloth Room units: cm and frames. So, when you set D to the default 0.1, the cloth on the tilted box is accelerated with 1.089*sin(z) – 0.1*cos(z), which determines its speed and displacement. Now I can appreciate why Dynamic Friction has a max on 1.0, where the critical tilting angle is about 45*. More is quite meaningless, it would lock the cloth to the object in about all positions.
Poser Cloth Density had no effect on these findings, tested from 0.001 to 0.500. As in the theory. That’s something.

When G*sin(z) – D*cos(z) < 0 the net force on the cloth is negative, and the cloth eventually would stop moving, or vice versa: doesn’t even start. At least, that’s the idea. Not starting, in formula: S>G*tan(z) introduces S for Static Friction.

I observed that the formulas did not hold very well at low cloth speeds, where Dynamic and Static frictions both became a factor of influence. This was not the case at higher cloth speeds. I observed that no value for Dynamic Friction could bring the cloth to a stand still once moving, nor could prevent it the cloth from starting to move. Only Static friction could do that. The other way around, the Static Friction parameter has no effect in the “tilted table” experiment, except for low dynamic friction (<0.1), small tilt angles (< 20*), low speeds (I sometimes needed over 3200 frames in animation / simulation). From this and the above I infer that static friction is something extra, having noticeable effects at zero or low speeds only. I can expect a minor effect from stretch, as gravity stretches the cloth, and therefore it moves the center of mass. I then guess that the Static Friction is here to prevent the entire cloth from moving as well.

In other words, it’s Static Friction at zero speed, some mixture of Static and Dynamic at low speeds (1-10 cm/frame) and Dynamic only for higher speeds. The figure intends to give some idea of this (red: static, blue: dynamic, green; total).

In the mixture, Static became noticeable only at low Dynamic values (< 0.1) or at Static values close to the critical G*tan(z) one, where it prevents the cloth from moving at all and velocities are very low.

Two issues in here, on the mixture at low speeds:

• Determining Static friction at low speeds at low Dynamic Friction is very hard. It either requires very small tilt angles or precise observation in the few frames after the start of the cloth movement. Not very accurate, that is, and therefore all conclusions get drowned in a sea of measurement errors.
• unfortunately, the low speed 1-10 cm/frame = 30-300cm/sec range mentioned above is the one for clothes under normal moving conditions. Girl getting seated: 60cm/sec=2cm/frame. Default cloth falling due to gravity: 245cm/sec=8cm/frame. See Density & Air Damping (previous section) and
  Cloth-the Sim Side on air damping and (animation) speed limits. That’s bad luck for simulating clothes. We need both the Frictions.
  When I use or analyze python scripts that address the Cloth Room, I find a parameter VelocityCutOff associated with the Frictions, set to 30. Sounds like 30cm/sec = 1 cm/frame to me. Perhaps that’s the moment Dynamic Friction kicks in.

www.hypertextbook.com/facts and a few other places on the net present acceleration and static numbers for human skin and cloth-to-cloth like info. These vary between 0.65 (skin to metal), 0.70 (skin to paper, cloth to cloth) and 0.75 (skin to plastic). Other reasonable values for Poser use (cloth, skin) ranged from 0.3 to 0.6. The latter suggests that the Poser default for Static, 0.5, is reasonable. The former suggests that the Poser default 0.1 for dynamic friction is far too low. Unless we stick to the idea that de default stand for light silk. Silk is extremely smooth, and perhaps 0.1 is fine for silk over a polished wooden table or a lacquered car surface. It does not represent normal clothing over human skin though.
Next to that there are hardly relevant numbers available for our Poser use in the literature. Lots of industrial materials, and long / heavy duty applications. Like tire rubber on concrete, like steel on steel (bolts), and so on. In general, static values are a bit higher than dynamic but not too different. Values for industrial materials can vary wildly: from 0.04 (Teflon) to over 1 (iron to iron on railroad tracks).

From the S = G*tan(z) formula, setting the angle z for a tilted plank and altering Static Friction till the cloth just did/did-not started moving revealed values for Static Friction that did not resemble any physical meaning to me.

Cloth Friction

Then I had a peek into Cloth Friction. I clothified the plank itself, put all its vertices in a choreographed group, combined both the plank and the former piece of cloth in one simulation and – of course – I checked the cloth-cloth collision box.
The first results were a nightmare, as the cloth started to wrinkle and crumble, and fell through the clothified plank. This was repaired by raising the fold-resistance (from 5 to 100).

Since then, I have not found any effect of varying this friction parameter on the position or speed of the cloth at any moment. the results are different from Static or Dynamic, but the same for all values of the Cloth friction. Some literature suggest 0.3 as a decent cloth-to-cloth value.
On top of all this, the SM page http://my.smithmicro.com/tutorials/2313.html does not show any differences between values 0.001 and 0.9, and notices that the effects will mainly be visible in animation. Well, not in mine!

So my question to you all: has anyone seen any noticeable effects in animation or stills of changes in this parameter? because if not, no investigation can be done. And then there is no need to, as any value will do for anything.

Engineering stuff

The concept of Static and Dynamic friction is sort of understood by most people: Static holds the cloth in place until the ‘driving force’ gets too large, and Dynamic works against the driving force when the cloth is moving. Both are independent of cloth density, and Dynamic friction is independent of cloth speed (unlike for instance air damping).

Wikipedia has good info on the theory, in case you need some. Friction is a force, which works against the force that drives the cloth over a surface. The friction is proportional to the force which presses the cloth onto the surface. When the surface (e.g. a plank) is tilted, the driving force from gravity reads F = d * S * g * sin(z) for density d, cloth surface S, gravity acceleration g and angle z with the horizon (flat = 0°). And the friction force reads F = f * d * S * g * cos(z) for friction parameter f (as the rest equals the force down to the box).

At the angle where static friction just prevents the cloth from moving, both forces are equal, and all collapses to f = tan(z), having most values between 0.3 and 0.6 in real nature, as I found while wading those loads of physics tables on the net. Values for f larger than 1 are rare.

For dynamic friction, we’ve got Coulombs Law stating that the force is independent of the sliding velocity.
So, when the cloth moves, we should see a constant acceleration of the cloth with gravity force F = d * S * g * sin(z) minus friction F = f * d * S * g * cos(z), over the cloth mass d*S. Hence, the acceleration reads g * [sin(z) – f*cos(z)].

For a given angle z this is like free fall along the boxes surface, so we might expect

• falling speed v = g * [sin(z) – f*cos(z)] * t (t for time) and
• distance s = 1/2 * g * [sin(z) – f*cos(z)] * t².

Correcting for unit conversions, and noting that the friction parameter is a ratio between forces and therefor unit-less, we should be able to interpret the Poser measurement results. So I created an animation, 240 frames in total, and made the box rotate along the Z-axis in the first 120 frames, up till the angle of interest, say 30 degrees. I had to do this slowly, because otherwise the cloth would get launched. And it’s a good idea to zero out Air Damping to prevent hovering.

First I turned down Dynamic Friction, till its lowest 0.0001 value. Then I started playing with the Static friction, till I found the critical value that started / stopped the cloth from moving when the box was at its largest angle, and the cloth was on top. Just a fraction less and the cloth started moving. That ‘critical value’. Each angle of interest has its own critical Static Friction value, and vice versa. These were my results:

This means that at a tilt angle of 30 degrees the cloth started moving when the Static friction value came below 0.13, while physics theory says that at that angle the friction value is 0.58 (=tan(z)). So, the Static friction does not resemble anything in real life to my current knowledge. It prevents the cloth from moving indeed, not effected by Dynamic friction, but there is no relationship (discovered yet) between measured values and the literature ones. The concept fits but the model does not. So those who want to match cloth behavior to life, need a re-direction.

A similar experiment could be done for Dynamic Friction. Same setup, I took a Static Friction value a bit below the critical one, so the cloth would move but not before it had reached the top at frame 120. I varied the Dynamic Friction value and noted the frames (the time) that the cloth passed halfway and the end of the box. Higher friction values made lower speeds and therefore larger pass-by frame numbers.

After measuring the size of the box I could infer the speed, meters per frame or per second, as a result from the dynamic fraction, at that angle limit of the box. This is a shipload of details, so I’m not posting them. In the meantime, I noticed a few effects while playing with the parameters.

• Density has no effect on friction, at the larger angles. This is physically correct. But it does have effect at the smaller angles.
• The stiffness parameters (fold/shear/stretch) do not have effect (which is correct), until the stiffness passes values like 400.
• In some cases with large parameter values, the cloth started rotating while coming down.

I have no physical interpretation for any of these. It might be something in the simulation algorithm. But most important, while I got neat looking results of cloth displacement over time, I could not make any physical sense out of it.

To summarize, my Poser Cloth Room experimental measurements do not fit physical theory. That’s it, plain and simple. The static friction angle vs critical value list does not follow the simple f = tan(z) or anything alike. The dynamical friction values do lead to neat distance vs time relationships, but not the one from Coulombs Law.

After a (long) while of puzzling, I finally got the message. Dynamic Friction in Poser is independent of speed and density (Poser matches theory), but it’s not a ratio between forces but a material-dependent acceleration by itself. So 1 stands for: 1 cm/frame² which is comparable to the 1.089 of the gravity constant in Cloth Room. It won’t vary when I alter the tilting angle of the plank in the experiment. This matched my findings for higher cloth speeds (> 10 cm/frame) only. At lower speeds the effect of Dynamic Friction decreases and the results are effected by Static Friction as well. Which might be a good idea from a simulation point of view, but it’s not according to the books, and it does not help my determining of values and Poser behavior.

So, for Dynamic Friction we’ve got an acceleration D instead of the f*g*cos(z) on the plank, and units are cm and frames. Now let’s face it: when a sleeve of a shirt moves over my arm, and my arm is held under a small angle (say < 15°), the sleeve is not going to move in a way that Dynamic Friction becomes important. And when I hold my arm under a large angle, say >30°, the sleeve comes loose a bit which reduces the effect of Dynamic Friction too. This means that in practical cases where Dynamic Friction can be relevant, g*cos(z) has a value between 0.95 and 1.05 (note that g=1.089 in cm and frames). And when we allow for a range 0.90 – 1.10, we’re considering all tilt angles from 0 to 35°.

The conclusion from that is, that within a 10% accuracy, I can use the literature values (for friction constant f) for the Poser dial value D. That’s a breakthrough. And according to www.hypertextbook.com/facts and some other places on the net life values vary between 0.65 (skin to metal), 0.70 (skin to paper, cloth to cloth) and 0.75 (skin to plastic). If you find reasonable values somewhere else, you can just plug them in (and please tell me about them). Industrial values are plenty (teflon 0.04, iron-on-iron 1.0 or more, good for railroad tracks), but normal cloth over normal skin is scarce in the literature.

From this we can infer that the Poser default value 0.1 is not too bad for silk over a lacquered wooden table, but is far too low for cloth over cloth or skin. Good for Cloth Room, not too well for Clothes Room :). We might guess some values as well. Rubbing my arm with rubber eventually burns and hurts, so that’s a high value (0.85). Leather is a bit less (0.75), then comes burlap and wool (0.70), then the normal linen and cotton shirts (0.65), and then the smooth stuff, like flannel (0.55) and silk (0.50).

Static friction in Poser is entirely different from real life – as I understand it – , but we’ve got a graph now that shows theoretical and practical values in one. In literature, static friction values for cloth and skin (hardly to find, but nevertheless), ranged from 0.3 to 0.6. Similar literature however states that the Static value is a bit higher than for Dynamic, as can be expected from theory as well. Using the graph, 0.3 indicates a critical angle between 15° and 20° (red curve), which indicate a Poser value of say 0.05 (green curve). The same way, a literature value of 0.6 indicates a critical angle of about 30° which indicates a Poser value of say 0.15. And when I find a Dynamic friction (in literature) of say 0.7, and I expect the accompanying Static friction to be a bit higher (say 0.8) then this translates to a critical angle of 35°-40° and a Poser value of 0.4.

From this we can infer that the Poser default 0.5 is not too bad for cloth over a wooden table but could be reduced to say 0.35 for cloth over cloth or skin. But for smooth materials with Dynamic values as low as 0.5, the accompanying Static must be reduced to 0.15.

Another observation is that Static plays a role on moving cloth as low speeds. This is not what one expects from the books. And unfortunately, this “low speed range” (1-10 cm/frame) is very common in our clothing use of the Cloth Room. From getting seated very gracefully (0.5 cm/frame) to a speedy cartwheel (20 cm/frame), all normal animation fits in this range.

So, in order to improve image or animation results one not only has to take care of Dynamic but of Static also, while the meaning of the dial-values for both are very different. Since friction plays a relevant role in the interaction between cloth and figure, this is the place where our artistic / alien experience or gut feeling will creep in., and Real World should be considered overrated.

Finally, Cloth self-friction is a mystery to me as no change in value provides any effect on any result in animation or final image. I have no fit for even the concept.

The Cloth Room Resistances for Fold, Shear and Stretch are determined by the fibers used, and the weave in which the fibers are combined.

The weaves – some of them shown in the next page figure – are hard to make calculations for. Fabric parameters themselves are published and available on the net, but only for the heavy duty / high performance ones. Look for fabrics for game sailing or surfing or parachutes, and you’ll find plenty. They even use different weaves for the different sails on the same ship. Look for fabrics for normal clothing, and you’ll find none. Google for “stretching jeans” and you’ll get lots of tips how to make you pants fit better. Google “folding cotton” and you’ll get a course in fancy towel folding.

But that’s for single fiber, and usually fibers are spun into yarn, with thicker threads, thicker cloth and higher tex values. For various silk fabrics, values can be found like:

• Gauze     12 to 20 gr/m²
• Organza     15 to 25 gr/m²
• Habutai      20 to 70 gr/m²
• Chiffon      25 to 35 or 50 to 70 gr/m² (double thickness)
• Charmeuze     25 to 125 gr/m²
• Crepe de Chine     50 to 70 gr/m²
• Raw Silk    150 to 175 gr/m²

Note 1: thickness affects appearance: 10 gr/m² is semi transparent, 25 gr/m² is translucent, 100 gr/m² is opaque.
Note 2: To put values in perspective: Poser default cloth density reads 0,005 gr/cm² = 50 gr/m².

Now we can start to pull the fiber. The result of that depends on the force per fiber-cross section, in Newton per m², or more practical: N / mm². But since fibers can come in various thicknesses, N/tex is the preferred material constant. And the amount of N/tex times the Specific Weight (in gr/cm³) of the material results in kN/mm²:

5 N/tex * 1.2 gr/cm³ = 5 N / ( 1 gr / 1,000,000 mm) * 1.2 gr/ 1000mm³ = 5 * 1,000,000 / 1000 * 1.2 N/mm² = 7 kN/mm².

At low forces, the elasticity or modulus of the material is the ratio between the stretch in % and the force in N/mm2. At high forces, a specific amount of N/mm2 will make the fibers snap. By doubling the thickness of the fiber (thread, yarn, cable) one can quadruple the strength of it.

Since measurements usually have a more scientific / engineering background instead of an industrial one, fiber strength is expressed in MPa (MegaPascal, 1 Pa = 1N/m²) or psi (pound/square inch).
1 N/mm² = 1 MPa = 146.25 psi; 1 kpsi= 6.84 MPa.

Values for polyester (www.ides.com):

• Specific weight (aka “gravity”): 1.24 to 1.48 g/cm³.
• Tensile Modulus (stiffness): about 300,000 to 400,000 psi or: 3000 to 4000 psi per % elongation
  that’s 3000 to 4000/146.25 = 20 to 30 N/mm² per % (or say 25/1000/1.25 = 0.02 N/tex)
  The breaking strength is 5000 to 9000 psi or about 35 to 60 N/mm² which is about twice as much, so polyester is not going to stretch very much.

Steel has about a similar stiffness (20 N/mm per % elongation) and due to its high specific weight (8 g/cm³) a low 0.0025 N/tex value: you’ll get less stretch resistance per pound of material. But it stretches nicely till say 200 MPa and breaks at 400 MPa. So steel can handle far larger forces than polyester, and stretches up to 10%.
Lead for instance is much more deformable, with 1.6 N/mm² per % elongation.

Teflon / PTFE: 2.2 gr/cm³, breaking strength 28 N/mm²; it’s a heavy, brittle material but it has an extremely low friction: 0.1 which makes it fine for surface coatings.

Another example: Kevlar (as in bullet proof vests): The modulus is about 60N/mm per % strain (twice as strong as polyester), but breaking at 2N/tex, and with a SW = 1.45 g/cm³ we get 2900 N/mm². That’s why it’s in bullet proof vests: the projectile has to break the fibers and that slows it down considerably, it’s say 10 times stronger than steel. Human skin breaks at say 20 N/mm² so that’s why we need the protection.

High performance cabling for shipping, like Astra: 0.97 gr/cm³ (so it floats on water), and with 0.15 – 0.20 N/tex it can handle about 150 N/mm² while stretching only 1%. And is can stretch a lot (30% or so) while not breaking. This is the stuff that keeps ships to the quay, especially when using over 30 mm thick cables.

Generally speaking, the stiffness for high performance cabling is about 100 N/mm² per % elongation. For most materials that we make to cover and protect our body, the stiffness is about 10. For natural clothing materials, (wool, cotton) it’s about 1. I needed tens of pages on the net to gather and combine information like the above. And I still have nothing reasonable for fabric itself, I’ll have to construct that.

1 meter of cloth required about 1000/(1.5 d) threads in one direction, and about the same in a perpendicular direction, using thread diameter d in mm. When a single thread has a stiffness S (eg 25 N/mm² per % elongation) then 1 m of cloth has a stiffness of (1000 S)/(1.5 d)*(3 d²/4) = S*d*500 (pi rounded to 3 as the 1.5 thread distance is a quesstimate anyway).

I also stated above that 1 m2 of fabric has a weight of 4T/3d, in gr/m², diameter d in mm, T in tex about equal to 1000 d², so the weight in gr/m² equals about 4.000 d/3 (d in mm). In Poser, I concluded earlier that the ratio Stretch Resistance to Cloth Density is typical for the material, an in this case it reads (S*d*500) / (4000 d/3) = 1.5 S / 4. In nature, that is say 10 and in Poser (default values) that is 50 / 0.005 = 10,000. Let’s check units again.

Assume d=1mm, then 1 m cloth takes 1000/1.5 = 667 threads, each having a 3/4 mm² cross section. Stiffness S = 25 N/mm² per % elongation then turns into 667 * 3/4 * 25 = 12,506 (N/mm² per %). The amount of fiber is 2* 667 m * 3/4 mm² = 1000 cm³, and hence weights 1340 gr (/m²). Which sounds okay, considering a 1mm thick thread resulting in a say 2mm thick cloth. The stiffness / density ratio is 12,506/1340 = 9.33 about 10.

In Poser, cloth density is not measured in gr/m² but in gr/cm². This makes a factor 10,000. Second, the default stretch resistance is known to produce far too elastic cloth in the simulations, 500 might do far more realistic and in line with the real values we’re using here (although it might elongate the sim itself). So, in Poser: 500 / (0.005 * 10,000) = 10 again.

In other words, the Poser Stretch Resistance is: (1.5/4 * 10,000 =) 3750 * S * D for stiffness S (in N/mm per %) as found in the literature, and cloth density D (in gr/cm² as set in Poser). Realistic densities range from 0.025 to 0.075 despite the 0.005 default representing silk. Realistic stiffness values are:

• Rubber        0.3 – 1
• Natural fabric    1 – 3 (wool, cotton)
• Enhanced    3 – 10 (cotton / polyester etc)
• Artificial    10 – 30 (nylon, …)

A reasonable cloth value is: 4 (enhanced cotton) * 0.03 (thin shirt) * 3750 = 450. And when that turns out to be too high for a proper sim, reduce both Resistance and Density in sync.

Since shearing is meaningful for cloth only, and not for individual fibers, and has less industrial implications and applications compared to stretch, there is far less research done and there are far less values available. So my suggestion is to use values below the Stretch Resistance. Just a bit, except for those special cases that hardly stretch but shear a lot, like chain mail vests. Then Shear Resistance really is smaller than the Stretch one.

Folding has a similar story. The industry wants to know how many times a fiber can be folded before it wears out and breaks. Resistance to folding is futile. Actually, when folding a fiber with thickness d (diameter), it experiences a local stretching of 100 * d/R. 100 for making the result into %, and R is the folding radius, much larger than d.

As can be seen in the figure, the core of the fiber makes a turn forcing the outer part to relatively stretch d/2R and the inner part to shrink d/2R as well.

A sharp fold means a small R and much local stretching in the fibers. And we discussed stretching. Thicker cloth means thicker threads so d/R goes up for the same sharpness of the folds: it takes more effort to make them. Which material is a better folder? Hard to say, a better question is: which material folds sharper for the same fiber thickness and the same force applied?

Rubber seems a bad folder as it’s hard to make the folds really sharp, but what if it’s equally thick as a cotton shirt? Personally, I tend to follow the stiffness values as presented above. Rubbers fold better than natural fabrics over enhanced fabrics over artificial materials, at the same cloth (mass) density.

Since folding only affects a portion of the cloth instead of the whole cloth, using a Folding Resistance which is a tenfold smaller than the Stretch Resistance (as demonstrated in the defaults) might be a good idea.

Download this tutorial in PDF format (0.4 Mb).

As a decent mutual understanding is key in maintaining good relationships, I wrote Poser Features in Perspective to give you some historic background on various Poser functions that receive a lot of debate. Cloth Room, FireFly rendering and the evolution of the Vicky and Mike characters, for instance. Especially Poser users discussing the future might be interested in some history.

For those curious about the peculiarities of cloth simulation in general, I added Cloth Simulation in Perspective. It’s mainly about the behavior of 3D meshes for cloth, so especially Dynamic Garment Makers (virtual tailors) might be interested.

The history of Poser is rather well documented in Wikipedia. Just a brief overview:

1	1995	Fractal design
2	1996	Fractal design	Props, Animation
3	1998	MetaCreations	User Interface (the Bryce-like), Expressions, Hand poses
4	1999	MetaCreations	Sketch render, Transparency, Conforming clothes, Magnets
ProPack	2000	Curious Labs	Python scripting, custom rigging (now: setup room)
5	2003	Curious Labs	Firefly render, Collision detection, Dynamic hair & cloth
6	2005	e-Frontier	OpenGL, IBL, Cartoon render
7	2006	e-Frontier	Talk designer, multithreading, HDRI, Morphing brush, universal poses

MetaCreations was a merger of the people from Poser, from Bryce, from Painter, from RayDream/InfiniD, from Kai’s Power Tools and alike. Thanks to this, Bryce was able to handle Poser files from the early days on, and thanks to Kai Krause, they both have a similar user interface. When MetaCreations broke up, Bryce and Painter went to Corel who later sold Bryce to DAZ. InfiniD went to Eovia to become Carrara, which later ended up at DAZ as well. The Poser people continued as Curious Labs.

Establishing Poser 5 however turned into a shear disaster (well described by John (Vanishing Point) Hoagland himself in http://www.cocs.com/poser/poser5mess.htm) and e-Frontier took over. After a while they sold their entire American branch to Smith Micro (founded by William Smith Jr). The Japanese branch is still known for the 3D modeler “Shade” and still represents the Japanese version of Poser. From then on Poser is in the hands of Smith Micro, Poser Pro gets introduced, and functionality has increased a lot since.

For a better understanding of the advanced features like Cloth Room and FireFly, it pays off to elaborate a bit on that hectic period around the turn of the century. Let’s take a look from the other side.

Reyes

In January 1996 the writer/producer Jorge Martinez Reverte, Javier Reyes and Jose Maria De Espona formed a company REM Infografica, based in Madrid, Spain. REM was the acronym of Reyes Espona Martinez. Martinez became CEO, Reyes became Technical/R&D Director and De Espona became the Art & Production director for the 3D Models Databank. (source: www.deespona.com/personalweb).

A sequence of splits and mergers (1998) moved the modelbank to Viewpoint (later: Digimation), created Next Limit (RealFlow) and also Reyes Infografica, known from 3DS Max plugins like Cloth:Reyes, Cartoon:Reyes, NPR:Reyes and more. In 2000 the latter sold its plugin technology for use in Poser. Cartoon:Reyes became Poser Toon render (the Sketch render was already available in Poser 4), NPR:Reyes became the Poser FireFly render, Cloth:Reyes became Cloth Room and so on. Javier Reyes himself continued with Virtual Fashion, until that came to its own end as a product (say 2009).

Some background references:

• http://www.cgarena.com/archives/interviews/3daliens/interview.html on the foundation of Next Limit
• http://forums.cgsociety.org/archive/index.php/t-725233.html Reyes Infografica doing plugins for Max 2 (1998, I was into 3DS Max myself, those days).
• 3DS Max moves to Kinetix (Max 3, 1999) which then moves to Discreet (Max 4, 2000). From 2001 on, the Reyes plugins were not supported anymore
  http://forums.cgsociety.org/archive/index.php/t-725233.html
  http://forums.cgsociety.org/archive/index.php/t-1006.html
• 3DS MAX 5 introduced a completely renewed set of… rendering features.

So now we know where those Poser modules came from, and why creating Poser 5 took so much trouble: a lot of (Spanish?) 3DS max plugins had to be integrated in the Poser 4 framework. In the meanwhile, sometimes some confusion passes by.

The rendering module
The NPR:Reyes (NPR = Non Photoreal Render) aka FireFly render is based on the initial Renderman REYES technology, where REYES is an acronym for Render Everything Your Eyes (can) See. The Reyes from Infografica is just a normal Spanish name. In the NPR:Reyes product, the two came together.
REYES was a serious improvement over the scanline rendering (Poser 4, 3DS Max) without the enormous calculation times from the raytracers in those days, and with the ability to chop rendering tasks in pieces to support large scale projects. It did not support extensive raytracing (*) but offered speedy alternatives (environment mapping) instead. Later on, Pixar enhanced the Renderman techniques by adding explicit raytracing to create their own PhotoRealistic Renderman toolkit.
So it might come as a shock to you, but FireFly is not raytracing very well. By design.

(*) for the tech’s amongst you: classical raytracing techniques scatter rays of light throughout the scene, and must consider the scene, and the objects, as a whole to do so. The REYES algorithm on the other hand chops a scene into chunks (buckets) and then into very tiny pieces (micropolygons) in an early stage. So both treat the scene geometry in opposite ways. As a result, REYES based renderers have problems with raytracing, and raytracing renderers have problems with performance.

A view on characters

So, the introduction of Poser 5 was a milestone in its history, and a heavy one. Next to the software and its functions, it had impact on content and future developments as well. Up till then, DAZ had created the Vicky and Mike characters (versions 1 and 2) based on the P4 female and male, which as such were Zygothe products. The turnover to Poser 5 brought some serious licensing issues between MetaCreations and DAZ, and the latter decided to go their own way.

This own way introduced the unimesh geometry, the wish to create all characters from one single mesh. Vicky and Mike 3 introduced that concept, soon to be followed by Stephanie 3 which was a real-person body scan translated to the unimesh. DAZ also had their own view on the software, which brought us Daz Studio consisting of a free base with paid plugins – just a completely different marketing concept compared to Poser.
Boths DAZ views developed, and after a successful rebuild of Vick and Mike 4 using the new modo modeler, and after successfully turning Girl 4, Steph 4 and so on into morphs of Vickys mesh, DAZ launched Genesis – the new generation unimesh, with all known figures (Vick and Mike 5 included) provided as morphs of that base mesh, and including a serious Poser contender Daz Studio 4, at the turn of 2011/2012. The weight-mapping mechanisms for smoother posing forced Smith Micro into similar features for Poser 9 / Pro 2012. But mainly, the full features of the new DAZ characters could not be deployed in Poser at the fullest, you needed DS4 for that.
This came as a serious chock to the Poser community. Being “Poser-compatible” was not the default anymore.

There is always more (on clothing)

Around the turn of the century, Serge Marck published his site www.poserfashion.net (before it got hacked, you can find the Original in Internet’s WayBackMachine). He published clothes for Poser 4 (conforming), Poser 5 (some dynamic for V3) and Poser 6 (dynamic, V4).He was into cloth simulation for some time already, and discussed SimCloth, Cloth:Reyes, ClothFX and Maya/Cloth. Apparently the relevant products in those days.

SimCloth is still around as a Max plugin. It’s opensource, so just go http://www.spot3d.com/simcloth/ and get the code, if you like. That is, if you want to find out about the internals. It’s created by Vladimir Koylazov (Vlado) in 2000 – 2002, and got a serious update in 2005. Vlado himself works at the Chaos Group, home of the VRay renderer. Small world.

ClothFX is announced (Jan 2004, www.thefreelibrary.com) as “the” cloth simulator for 3DS MAX, and referred to as the new name for Stitch. This one gets a Stitch Lite equivalent “compatible to Max4, Max5 and Stitch” (Feb 2003) and owned by Digimation. Didn’t they get the REM Infografica Modelbank also? During the issue of 3DS Max 7, ClothFX was distributed for free and since Max 8 it’s part of the program stack. According to the current 3Ds Max manuals, ClothFX is a trademark from Size8 software. Their single page website refers to TurboSquid where the free ClothFX was distributed.

Cloth:Reyes ended up in Poser Cloth Room. According to the credits for Poser, the cloth simulation was written by Size8 Software also. Note that Virtual Fashion was a garment maker, like Marvelous Designer. Note that ClothFX introduced a garment maker into 3DS Max. And Poser got the simulation part only, and lacks a garment maker.

According to various posts on the net, and forum posts in CGSociety, debates around REM Infografica and Reyes Infografica were around patents on fluid and cloth dynamics. Apparently, not all the clothing guys went with Javier Reyes… perhaps Size8 is just another part of that original team. We’ll never know.

In the meantime, life goes on and so does cloth simulation. Halfway 2012 I found:

• Kinect Virtual Fashion – by MicroSoft. It uses MS Kinect / XBOX to measure up your body, and then you can dress up virtually. On Youtube: http://www.youtube.com/watch?v=s0Fn6PyfJ0I
• Cisco StyleMe Virtual Fashion Mirror, does about the same in retail environments, it’s a shopping business product
• ImageTwin, http://www.imagetwin.com/ – use Kinect to obtain your body shape.
• TC2, www.tc2.com – the guys behind the body scan technology

Now, given the body scan thing, where do you think that Virtual Fashion clothing comes from, since Javier Reyes teamed up with MicroSoft in various fashion conferences, and the software disappeared from the consumers software market in 2009?

Conclusion?

Now perhaps we can appreciate why FireFly is not that good in raytracing, and is very unlikely to become so in the near future. Till then we have to manage with translators (like Pose2Lux, or a Reality plugin for Poser perhaps?) into third party raytracers like LuxRender.

We also can appreciate why Cloth Room is very unlikely to undergo any drastic transformations. Till then we have to manage with a decent understanding of the tools at hand.

We also can appreciate why DAZ is demonstrating that Poser-compatibility is not an industry standard any more.

And finally, let’s not point at Smith Micro for the things they just inherited a few years ago.

Understanding cloth and having a mental model of the physics involved is necessary but not sufficient to make effective and efficient simulating systems. Creating those systems is a world in its own right. Especially those with an engineer’s way of looking at things might be interested in this mini tour through the deep down dungeons. Crash Course on Math & Physics (this page) and Crash Course on Sims & Settings (next)really are the math and physics loaded chapters. Any use of the underground escape tunnel brings you into Muppets Lab “where the future is made today”. You have been warned.

Download this tutorial in PDF format (0.4 Mb).

Some people immediately zap away when they see even a two-character formula coming along, others insist in getting the rough engineering treatment to enhance their understanding. This chapter is for the latter part of the audience, although I can recommend the conclusions to everyone.

I’ll start with some math first because 1) it simplifies handling the formulas and 2) in the forums people have stated to have some issues handling and grasping it. Second I’ll do the physics, from an electrical point of view. This gives the proper resulting formulas in an easy way, but it’s too far away from our actual simulations. So third, I’ll present the physics from a mechanical point of view. Similar formulas but much closer to our actual cloth simulation.

Then, fourth, I’ll consider the simulation algorithms themselves. Finally, I’ll present some conclusions that help you further in handling the Poser parameters and cloth simulation.

Complex Calculations

In order to handle straightforward object motion, steady currents and flows, I can simply deal with real numbers. But handling disruptions, oscillations, alternating current and more becomes a lot easier when I extent my repertoire to imaginary and complex numbers.
In that area, the magic bullet is called ‘i’ with the property i² = -1. I don’t have to understand it, it’s there, period. Multiplying a real number b by i turns it into the imaginary i*b (or: ib for short), and repeating the operation turns it into i*i*b = i²b = -b which brings me back into the real world again. When I mix a real number a and an imaginary ib I get a complex number a+ib, and I can do all adding and subtraction while keeping the real and imaginary worlds separate:
(a+ib) + (c+id) = (a+c) + i(b+d).
Like I can represent real numbers on a straight line, I can represent complex numbers in a simple plane. I can use dots or arrows to them, and adding and subtraction behave like simple adding and subtracting those arrows as in vector algebra.

Complex numbers however are not very friendly in multiplication and handling powers, exponentials and logarithms. As you can see in
(a+ib)*(c+id) = ac + ibc + iad + i²bd = (ac-bd) +i(bc+ad)
real and imaginary parts of the numbers get mixed, which might turn longer calculations into a sheer mess.

The vector approach however gives us an alternative. Instead of considering the x and y components of the vector, we can consider its length R and angle q with the horizontal axis. This makes a+ib equivalent to R*[cos(q)+isin(q)]. Adding and subtracting from this approach becomes a nightmare, but multiplication, division and more becomes easy. Multiplication is: multiply the lengths and add the angles, which follows in a straightforward way from classic geometry (I’ll save you the details).

To simplify our tool even more, I use natural exponents and logarithms to rewrite R to e^r (or r=ln(R) ), and especially (cos(q) + isin(q)) to e^iq. In other words, a+ib becomes e^(r+iq) where r=ln(sqrt(a²+b²)) and q= arctan(b/a). This is handy, since multiplication of values is equivalent to the addition of exponents, and taking powers is equivalent to multiplying exponents, so (e^(r+iq) * e^(s+it) => e^{[(r+s)+i(q+t)]} and [a+ib]^N => [e^(r+iq)] ^N => e^N(r+iq).

So, with this dirty trick, the issues of complex multiplication and power-lifting are reduced to addition and simple multiplication. That’s a gain.

This is the basic tool, now the application of it in physics. Alternating currents, oscillating movements and the like can be described as x(t) = Rcos(wt) where R is the amplitude, and w=2 pi f, for oscillating frequency f. Each time wt makes a multiple of 2 pi, or each time ft makes a whole number, the oscillation starts anew. Now it has become a small step to state that the oscillation we see is just the real world part of a complex movement, which also has an imaginary component in a world we can or cannot imagine J.
But as a whole, its described with x(t) = Re^iwt or even with x(t) = e^(r+iwt).

The main reason for doing this, is that we need time-derivatives (and integrals) like dx/dt to get speed, acceleration and more. But the classical approach presents us a plethora of sine and cosine functions, and we really need a lot of geometry to get understandable results. In the new approach, we don’t.

When x(t) = e^(r+iwt) then dx/dt = iw * e^(r+iwt), so d2x/dt2 = -w2 * e^(r+iwt), from position to velocity to acceleration,
but also ∫xdt = 1/iw e^(r+iwt) and so ∫∫xdt2 = -1/w2 e^(r+iwt) , from acceleration to velocity to position.

Going Electrical

In abstraction, basic physics considers a ‘field’ and a ‘thing’, and moving the thing against the field requires energy (from us or from the thing itself), while moving the thing along the field returns that energy back. One unit of field times one unit of thing make 1 Joule of energy, and if I do so every second it requires or generates 1 Joule per second or: 1 Watt of power.

Less abstract, in electricity the ‘field’ is electric potential (char: V) determined in Volt and the ‘thing’ is electrical charge (char: Q) determined in Coulomb. When such an amount of charge passes a measuring point within 1 second, we’ve got an electrical current of 1 Coulomb per second, or: 1 Ampere.
When I move such a charge to a place with a 1 Volt higher potential it requires 1 Joule (char: E, in formula: E=V*Q), and when I do so every second it requires a power of 1 Watt (char W, in formula: W = V*I). Especially this last formula on electrical power might hang somewhere in your memory, resulting from a physics class or so.

When I move a charge from one place to another, bridging a potential, it becomes harder for the next portion of charge to do the same. The source of the charges becomes short due to the displacement, or: anti-charged and as we know opposite charges pull each other. The destination of the charges gets a surplus or: gets charged, and similar charges push each other. In other words, by moving a charge across a field, it gets less interesting to continue, the field itself gets reduced. The ratio between these is understood as: electrical capacity (char C, measured in Farad).
In formula: dQ = C dV, when I move a charge dQ the field changes dV. When the device that includes the source and the destination of the charge is said to have a large capacity, this means that the displacement of large charges have little effect on the field.

Even when moving the charges hardly effects the field, the charge elements (e.g. electrons) have to bridge the gap between source and destination, collide to each other and to loads of molecules in between, and dissipate some heat. This is understood as electrical resistance (char R, measured in Ohm).
In formula: V = I*R or I=V/R, Ohm’s law. A large resistance is like having air (or less) between two poles of a battery, they are electrically isolated, there is hardly any current and no energy loss. A small resistance is like short-circuiting the battery with a copper wire. Lots of current, and the heat might even melt the wire. As current I = dQ/dt we see that first we had a relationship between ‘field’ V and ‘thing’ Q, and now we’ve got a relationship between V and the first time-derivate of the ‘thing’: dQ/dt.

So the next step is to investigate what happens with that second time-derivative, or: dI/dt. This just means: alternating current. When alternating current is applied onto a coil, it generates an electric field. This is understood as electrical induction, the fundament under dynamos, generators, turbines and the like. Char: F (after Faraday), measured in Henry (both did the discoveries at the same time).
In formula: V = F*dI/dt or dI/dt = V / F, a large induction generates a strong field from the alternating current.

Now, let me bring all the elements together. I’ve got a device with two poles, I apply an alternating voltage onto the poles, and the charges and currents in the device start working in parallel:

Working in parallel implies that I have to add the individual currents, so: (I1+I2+I3) = I total = Voltage / “Impedance” (Impedance is some kind of resistance for alternating currents and voltages, taking capacity and induction into account).

• Alt. Voltage    Vexp^{iwt}
• Capacity    I = dQ/dt = C * iw * Vexp^{iwt}
• Resistance    I = 1/R * Vexp^{iwt}
• Induction    I = 1/F * 1/iw * Vexp^{iwt}
• In parallel    I = [ C * iw + 1/R + 1/F*1/iw ] * Vexp^{iwt} = 1/IMP * Vexp^{iwt}
• So IMP     = 1/[ iwC + 1/R + 1/iwF ], after taking the inverse on both sides
  = iwR / [-w2 RC + iw + R/F], after multiplying with iwR on both sides
  = iwR [ (R/F-w2RC) – iw]/[ (R/F-w2RC)2 + w2], after multiplying with [ (R/F-w2RC) – iw]
  = w * [w/R + i (1/F-w2C)] / [(1/F-w2C)2 +(w/R)2]
• If R very small (short circuit), then 1/R becomes dominant and IMP => (w2/R) / (w2/R2) = R2/R = R
• If R very large (isolation), then IMP = iw / (1/F-w2C) and becomes quite large when 1/F-w2C => 0,
  that is: w2 => 1/FC. Then the impedance => R again.
  This w = sqrt(1/FC) represents the resonance frequency of the system, it behaves at a minimal energy loss.

Now we’ve got the essential formula, let’s apply them on a mechanical system.

Going Mechanical

The mechanical route follows the same approach. The ‘field’ is force (char F, measured in Newton) and the ‘thing’ is displacement (say X, measured in meter). Applying a force of 1 N over 1 m requires 1 J of energy, and applying that force over a route with a speed of 1 m/s requires 1 W of power. Note the similarities with electrical.

• A spring pulls and pushes, proportional to its stretch: F = S * X. The stronger the spring, the more force is required to stretch it (with the same amount of displacement). Spring strength does not have a specific name, it’s measured in N/m.
• Spring strength is not related to any mass, but when a mass is attached to a string, the force will generate an appropriate acceleration: F = M * a, Newtons Law, where a is d² X/dt², the second time derivative of the ‘thing’ we’re considering. M is mass, in kilograms.
• So we’ve seen forces proportional to distance X (the spring) and to its second time-derivative acceleration A (gravity like). So all we need to make it like electrical, is a force that is proportional to the first time-derivative of distance, which is: speed, or velocity v. This introduces: damping D as in F = -D*v. The faster you move, the more the force will work against you. Air-resistance is one example of them.
• Now we can make the step from electrical to mechanical, just by substituting the equivalent concepts
  • So electrical capacity C relates to 1/S spring strength
  • So electrical resistance R relates to 1/D damping
  • So electrical induction F relates to M mass
• And so w = sqrt(S/M) represents the resonance frequency of the system. The resonance becomes noticeable when there is only little damping. Strong springs with little mass with make high frequencies, loosening the springs and/or raising the mass will reduce the resonance frequency. Damping will kill the oscillations and will produce a stable result faster.

RESULT: IMP    = w * [wD + i (1/M-w²/S)] / [(1/M-w²/S)² +(wD)2], times S²M² at both sides:
= wSM * [wDSM + i(S-w²M) ] / [(S-w²M)² + (wDSM)²]
=> 1/D at the resonance frequency w = sqrt(S/M)

Mechanical systems and electrical systems do compare, but to a certain extent. Electrical components can be made quite ideal: capacitors with a good isolation and no leakage (extreme resistance), resistors with hardly capacity or induction by their own, inductors with metal kernels and so on. And those systems are pretty linear over a large range of values, from electron beams in a CRT monitor to outdoor flashes in a thunder storm, the same laws keep applying.

Mechanical components are far less ideal: springs do have mass and damping by themselves, and the stretching is far from linear. When the spring is made of an iron wire coil, there are upper and lower limits to its expansion or compression depending on the length and thickness of the wire used. So in fact the formula should read F = S₀ X + S₁ X³ + S₂ X⁵ + …

Odd powers only, as all forces work in one direction: against the displacement.
The same holds for damping, as can be found in any aero/fluid-dynamics class or textbook. For low speeds it’s proportional, but at higher speeds the additional terms kick in quickly: F = D₀ X + D₁ X³ + …

All this means that the math still can be done but that the final resulting formulas become longer and less friendly.

Conclusions

By looking at complex numbers in addition to normal, real numbers, I got tools for expressing fluctuations in a more elegant way. By applying them to electrical circuits with alternating current, I got the formulas for the “impedance” of a system responding to alternating inputs. By applying those formulas to a mechanical context, I got a descriptor for a mechanical system, responding to external forces.

I found that such a system is characterized by

• Mass (M), making it harder for a force to accelerate an object
• Damping (D), making it easier for a force to reduce an objects speed, and making the object lose energy faster
• Spring Strength (S), making it harder for a force to displace an object
• Resonance, the tendency to vibrate with a frequency sqrt(S/M). This is reduced by Damping.